728x90
반응형
1차원 배열의 구간 합
- 해당 구간의 값을 더해가면서 구간 합 배열에 넣는다. (S[i] = S[i-1] + A[i])
- i부터 j 까지의 합은 S[j] - S[i-1]로 구할 수 있다.
s = [0]
a = [1,2,3,4,5]
temp = 0
for i in a:
temp += i
s.append(temp)2차원 배열의 구간 합
- 2차원 배열에서의 구간 합은 (1,1)에서 (i,j)까지 영역의 모든 수의 합이다.
- 구간 합 배열은 S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j] 로 구할 수 있다.
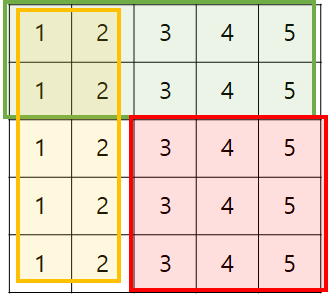
- 위의 예시에서 (3,3)에서 (5,5)까지의 구간 합은 빨간색 + 노란색 + 초록색 - 노란색과 초록색이 겹치는 부분이다.
따라서, 특정 구간의 구간 합은 S[X2][Y2] - S[X1-1][Y2] - S[X2][Y1-1] + S[X1-1][Y1-1]으로 구할 수 있다.
for i in range(1,n+1):
for j in range(1,n+1):
S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + A[i][j]
for _ in range(m):
x1,y1,x2,y2 = map(int, input().split())
print(S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1])'코딩테스트 > Python' 카테고리의 다른 글
| [Baekjoon] 1167. 트리의 지름 (1) | 2023.10.27 |
|---|---|
| [Algorithm] 다익스트라 (dijkstra) (0) | 2023.10.25 |
| [Data Structure] 트리 (0) | 2023.03.30 |
| GCD(Great Common Divisior), LCM(Least Common Multiple) (2) | 2023.03.24 |
| [Baekjoon] 1992. 쿼드트리 (0) | 2023.01.30 |