Bias란?
- 편향이라는 뜻의 Bias는 (실제값 - 예측값)의 평균이다.
- $[\hat{f}(x)] = E[\hat{f}(x) - f(x)]$
Variance란?
- 분산이라는 뜻의 variance는 예측값의 변화 정도이다.
- $Var[\hat{f}(x)]=E[(\hat{f}(x)−E[\hat{f}(x)])^2]=E[\hat{f}(x)^2]−E[\hat{f}(x)]^2$
Bias와 Variance의 관계
출처 - https://nvsyashwanth.github.io/machinelearningmaster/bias-variance/
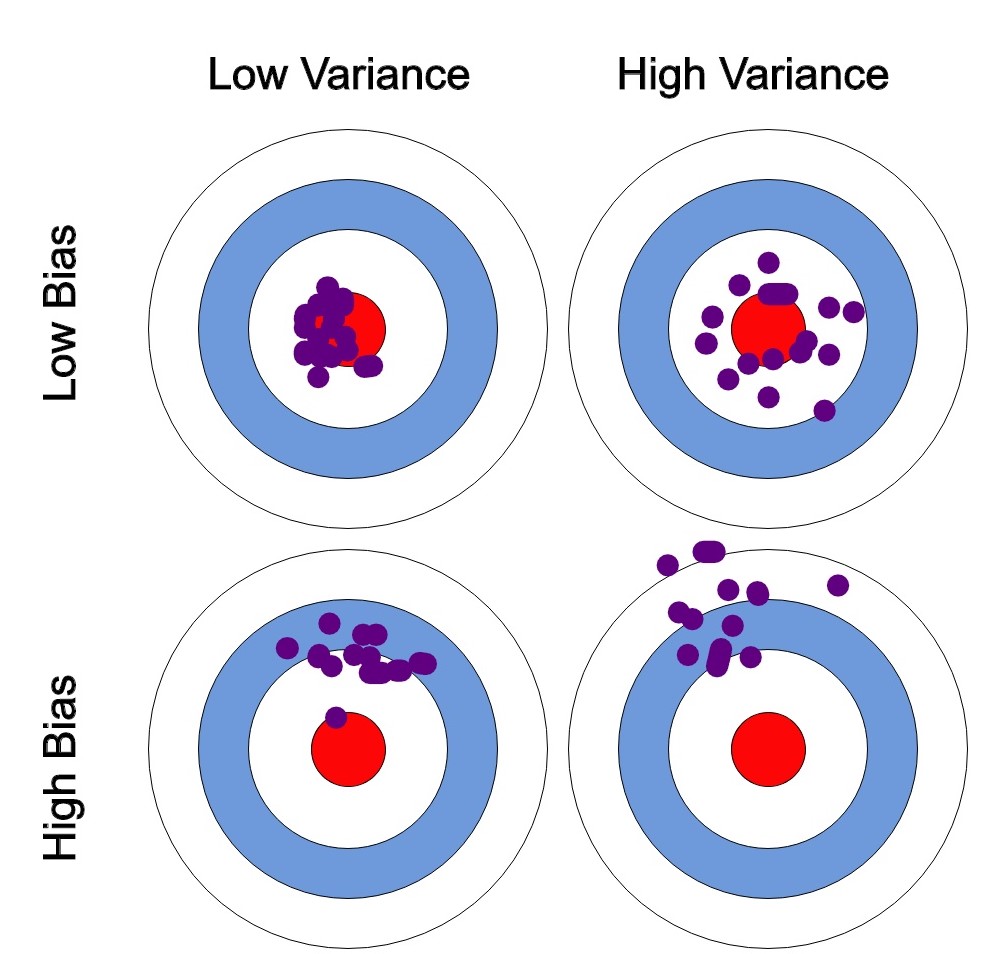
- low bias & low variance : 예측값이 정답에 가깝고(편향 낮음) 그 값들이 모여있다(분산 낮음).
- low bias & high variance : 예측값이 정답에 가깝고(편향 낮음) 그 값들이 퍼져있다(분산 높음).
- high bias & low variance : 예측값이 정답과 멀고(편향 높음) 그 값들이 모여있다(분산 낮음).
- high bias & high variance : 예측값이 정답과 멀고(편향 높음) 그 값들이 퍼져있다(분산 높음).
High Bias, High Variance 해결 방법
- High Bias
- Feature의 수를 늘린다. (큰 network 사.)
- regularization parameter의 $\lambda$를 증가시킨다.
- Train 시간을 늘린다.
- High Variance
- Training data의 수를 늘린다. (데이터 증강)
- regularization parameter의 $\lambda$를 감소시킨다.